解説
まず、座標をとってグラフを描きます。
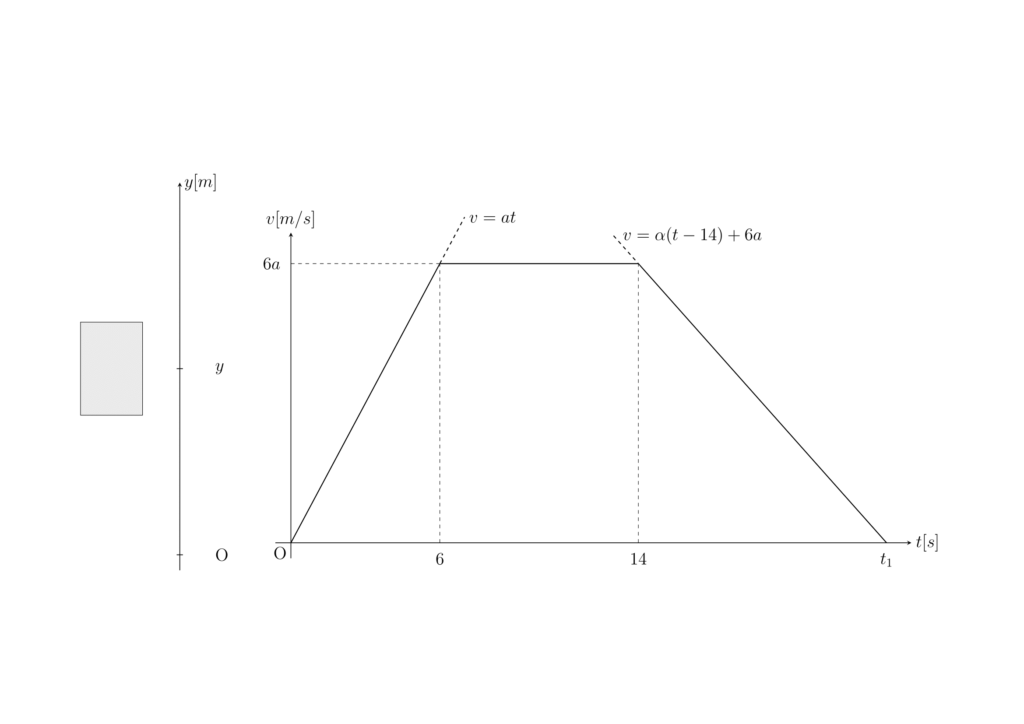
高校物理で微積は必要ないといわれる理由の一つに、出てくる関数が直線だということがあると思います。1次関数なので微積を使うまでもないということですね。まあこのシリーズでは使っていくのですが。
というわけでサクッとグラフの解説をしていきます。上のグラフでは区間 \(14\leq t\) の加速度を \(\alpha\) 、エレベーターが \(144 \ m\) 地点に到達する時刻を \(t_1\) とおきました。問題文から \(6+8=14 \ [s]\) は読み取りましょう。
ここからはこっちのほうが少し難しいですが、良問の風1とやることはほとんど同じです。難しいといっても数学の難しさに比べればなんてことないはずです。
(1)
\(0 \leq t \leq 6\) のとき、 \(\ddot{y}=a\) より
\begin{eqnarray}\dot{y}=\int a \ dt =at+C_1\end{eqnarray}
\(\dot{y}(0)=0\) より \(C_1=0 \unicode{x2234} \dot{y}=at \unicode{x2234} v=at\)
\begin{eqnarray}y=\int at \ dt =\frac{1}{2}at^2+C_2\end{eqnarray}
\(y(0)=0\) より \(C_2=0 \unicode{x2234} y=\frac{1}{2}at^2\)
(2)
\(6 \leq t \leq 14\) のとき、 \(\dot{y}=6a\) より
\begin{eqnarray}y=\int 6a \ dt =6a(t-6)+C_3\end{eqnarray}
\(y(6)=C_3=\frac{1}{2}a\cdot(6)^2=18a\) より \(\unicode{x2234} y=6a(t-6)+18a\)
\(y(14)=99\) とから
\begin{eqnarray}6a(14-6)+18a&=&99 \\ 66a&=&99 \\ a &=&\frac{3}{2}=1.5 \ [m/s^2]\end{eqnarray}
\(t-6\) のかたまりで積分しています。良問の風1で紹介した計算テクニックですね。慣れていきましょう。
ついでに \(6a=6\cdot\frac{3}{2}=9, \ C_3=18\cdot\frac{3}{2}=27\) ですね。計算は分数のほうがしやすいけれど、表記は小数のほうが数値感があってカッコいいです。
(3)
\begin{eqnarray}y(14)-y(6)=99-27=72 \ [m]\end{eqnarray}
区間ごとの \(y(t)\) をすでに求めているので、ただの引き算です。
(4)
考える条件は
\begin{eqnarray}\begin{cases}y(t_1)=144\\\dot{y}(t_1)=0\end{cases}\end{eqnarray}
です。 \(t_1\) では静止するので \(\dot{y}(t_1)=0\) です。これを読み取れないと解けません。
\begin{eqnarray}y=\int \{\alpha(t-14)+9\} \ dt=\frac{1}{2}\alpha(t-14)^2+9(t-14)+C_4\end{eqnarray}
\(y(14)=C_4=99\) より
\begin{eqnarray}y=\frac{1}{2}\alpha(t-14)^2+9(t-14)+99\end{eqnarray}
したがって
\begin{eqnarray}\begin{cases}y(t_1)&=&\frac{1}{2}\alpha(t_1-14)^2+9(t_1-14)+99=144\\\dot{y}(t_1)&=&\alpha(t_1-14)+9=0\end{cases}\end{eqnarray}
を解けばよい。
\(t_1-14=T\) とおくと
\begin{eqnarray}\begin{cases}y(T)&=&\frac{1}{2}\alpha T^2+9T+99=144\\\dot{y}(T)&=&\alpha T+9=0\end{cases}\end{eqnarray}
\begin{eqnarray}\frac{1}{2}\alpha T^2+9T+99&=&144 \\ \frac{1}{2}\alpha T^2+9T-45&=&0 \\ \alpha T^2+18T-90&=&0 \cdots\cdots\require{enclose}\enclose{circle}{1}\end{eqnarray}
\begin{eqnarray}\alpha T+9&=&0\ \\ \alpha T &=&-9 \cdots\cdots\require{enclose}\enclose{circle}{2}\end{eqnarray}
\(\require{enclose}\enclose{circle}{1}\), \(\require{enclose}\enclose{circle}{2}\) とから
\begin{eqnarray}(-9)\cdot T+18T-90&=&0 \\ 9T&=&90 \\ T&=&10 \unicode{x2234} t_1=24 \ [s]\end{eqnarray}
\begin{eqnarray} \alpha \cdot 10=-9 \unicode{x2234} \alpha=-0.9 \ [m/s^2]\end{eqnarray}
(5)
\((4)\) ですでに求めたので \(24 \ [s]\)


コメント