解説
図1のように座標を設定します。
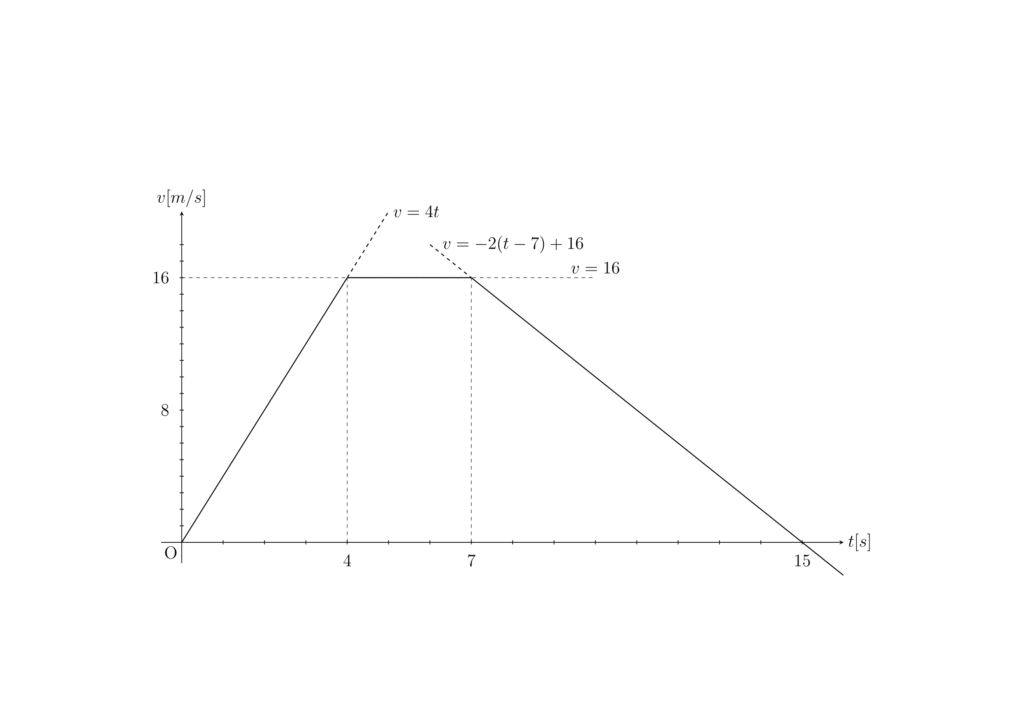
図2のグラフから
\begin{eqnarray}\begin{cases}0 \leq t \leq 4 \\ 4 \leq t \leq 7 \\ 7 \leq t\end{cases}\end{eqnarray}
で運動の様子が変わっていることが分かるので、これからそれぞれの区間ごとの運動を調べていきます。その過程でとくに初学者にとって難しく、少しテクニカルな計算が出てきますが、テンポを落とさないためにまずは触れずに調べ切ります。
設問に入る前にそれらについての解説を入れますのでまずは一通り目を通してください。
\(0 \leq t \leq 4\) のとき
\(\dot{x}=4t \cdots\cdots\require{enclose}\enclose{circle}{1}\) より
\(\require{enclose}\enclose{circle}{1}\) を \(t\) で微分して
\(\ddot{x}=4\)
\(\require{enclose}\enclose{circle}{1}\) を \(t\) で積分して
\(x=2t^2+C_1\) ( \(C_1\) は積分定数)
\(x(0)=C_1=0\) より
\(x=2t^2\)
まとめて
\begin{eqnarray}\begin{cases}\ddot{x}&=&4\\\dot{x}&=&4t \\x&=&2t^2 \end{cases}\end{eqnarray}
\(4 \leq t \leq 7\) のとき
\(\dot{x}=16 \cdots\cdots\require{enclose}\enclose{circle}{2}\) より
\(\require{enclose}\enclose{circle}{2}\) を \(t\) で微分して
\(\ddot{x}=0\)
\(\require{enclose}\enclose{circle}{2}\) を \(t\) で積分して
\(x=16(t-4)+C_2\) ( \(C_2\) は積分定数)
\(x(4)=C_2=32\) より
\(x=16(t-4)+32\)
まとめて
\begin{eqnarray}\begin{cases}\ddot{x}&=&0\\\dot{x}&=&16 \\x&=&16(t-4)+32 \end{cases}\end{eqnarray}
\(7 \leq t \) のとき
\(\dot{x}=-2(t-7)+16 \cdots\cdots\require{enclose}\enclose{circle}{3}\) より
\(\require{enclose}\enclose{circle}{3}\) を \(t\) で微分して
\(\ddot{x}=-2\)
\(\require{enclose}\enclose{circle}{3}\) を \(t\) で積分して
\(x=-(t-7)^2+16(t-7)+C_3\) ( \(C_3\) は積分定数)
\(x(7)=C_3=80\) より
\(x=-(t-7)^2+16(t-7)+80\)
まとめて
\begin{eqnarray}\begin{cases}\ddot{x}&=&-2\\\dot{x}&=& \dot{x}=-2(t-7)+16\\x&=&x=-(t-7)^2+16(t-7)+80 \end{cases}\end{eqnarray}
となります。
さて、これで運動を調べ終えたわけですが、
\(\require{enclose}\enclose{circle}{2}\) を \(t\) で積分して
\(x=16(t-4)+C_2\)
\(x(4)=C_2=32\) より
\(x=16(t-4)+32\)
\(\require{enclose}\enclose{circle}{3}\) を \(t\) で積分して
\(x=-(t-7)^2+16(t-7)+C_3\)
\(x(7)=C_3=80\) より
\(x=-(t-7)^2+16(t-7)+80\)
この2つの計算わかりましたか?まず、この計算の正体は置換積分です。ねらいは \(t=4, \ t=7\)
のときに積分定数だけ残るようにすることです。こうすると積分定数をその区間での初期値として考えることができます。
\begin{eqnarray}\int 16 \ dt\end{eqnarray}
\(u=t-4\) と置くと
\begin{eqnarray}\frac{du}{dt}&=&1 \\ \unicode{x2234} du&=&dt\end{eqnarray}
\begin{eqnarray}\unicode{x2234} \int 16 \ du=16u+C=16(t-4)+C_2\end{eqnarray}
\begin{eqnarray}\int \{-2(t-7)+16\} \ dt\end{eqnarray}
\(u=t-7\) と置くと
\begin{eqnarray}\frac{du}{dt}&=&1 \\ \unicode{x2234} du&=&dt\end{eqnarray}
\begin{eqnarray}\unicode{x2234} \int \{ -2(&t&-7)+16\} \ du\\ &=&-(t-7)^2+16(t-7)+C_3\end{eqnarray}
\((t-4), \ (t-7)\) のかたまりで積分してると考えてもらって大丈夫です。使っているうちになんとなくなじんできます。次に
\(x(4)=C_2=32\) より
\(x=16(t-4)+32\)
\(x(7)=C_3=80\) より
\(x=-(t-7)^2+16(t-7)+80\)
の部分ですが、 \(t=4, \ t=7\) は端点なので、1つ前の区間で求めた関数に代入しています。
\(0 \leq t \leq 4\) のとき \(x=2t^2\) なので
\(x(4)=2\cdot 4^2=32\)
\(4 \leq t \leq 7\) のとき \(x=16(t-4)+32\) なので
\(x(7)=16\cdot (7-4)+32=80\)
さて、いよいよ問題に入ります。とはいってもここまで整理できていたら瞬殺です。
(1)
これはもう調べてあるので、それぞれの区間の \(\ddot{x}\) を参照して
\begin{eqnarray}(ア)&=&4 \\ (イ)&=&0 \\ (ウ)&=&-2\end{eqnarray}
(2)
\(4 \leq t \leq 7\) の区間を参照して
\begin{eqnarray}x(6)=16(6-4)+32=64\end{eqnarray}
\(\unicode{x2234} (エ)=64\)
(3)
\((オ)\) はグラフから明らかに \(t=15\) のときですね。
全部数学でやりたいって人は平方完成しましょう。 \(t-7=T\) とおいて
\begin{eqnarray}x&=&-T^2+16T+80 \\ &=&-\{ T^2-16T\}+80 \\ &=& -\{(T-8)^2-64\}+80 \\ &=&-(T-8)^2+144 \end{eqnarray}
よって \(T=8 \unicode{x2234} t=15\) のとき \(x=144\)
\(\unicode{x2234} (オ)=15, \ (カ)=144\)
(4)
原点に戻ってくる時刻を \(t_0\) とすると
\begin{eqnarray}x(t_0)=-(t_0-7)^2+16(t_0-7)+80=0\end{eqnarray}
を解けばいいですね。 \((3)\) と同様に \(t_0-7=T_0\) とおいて
\begin{eqnarray}-T_0^2+16T_0+80&=&0 \\ T_0^2-16T_0-80&=&0 \\ (T_0-20)(T_0+4)&=&0 \\ T_0 &=& 20, \ -4 (T_0>15) \\ \unicode{x2234} T_0&=&20 \unicode{x2234} t_0=27\end{eqnarray}
\(\unicode{x2234} (キ)=27\)
\begin{eqnarray}\dot{x}(27)=-2(27-7)+16=-24\end{eqnarray}
\(\unicode{x2234} (ク)=-24\)


コメント